题目:给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。
示例 1:
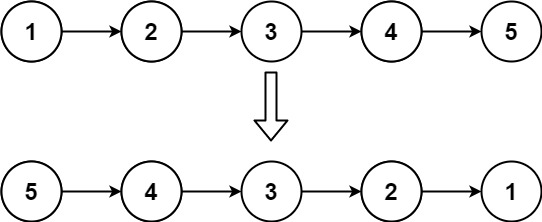
// 输入:head = [1,2,3,4,5]
// 输出:[5,4,3,2,1]
示例 2:
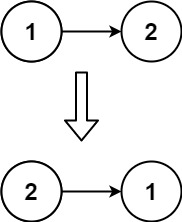
// 输入:head = [1,2]
// 输出:[2,1]
示例 3:
// 输入:head = []
// 输出:[]
提示:
- 链表中节点的数目范围是 [0, 5000]
- -5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
注意:本题与LeetCode 206 题相同。
思路分析
本题的第一种思路就是我们可以使用迭代法来解决,本质上也就是遍历链表。比如假定链表:
// 1 -> 2 -> 3
反转过后结果应该是:
//3 -> 2 -> 1
链表的反转跟数组不同,链表反转,我们可以约定三个指针,即前一个节点prev指针,当前节点cur指针,下一个节点next指针。所以反转的话本质上就是交换三个指针的位置。我们用prev = null开始,cur = head。然后如果cur节点不为空,我们就开始遍历,然后将当前节点的下一节点也就是next设置为prev,prev设置为当前节点,当前节点设置为下一节点,即可解答本题。代码如下:
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
let prev = null,cur = head;
while(cur){
//获取当前节点的下一节点
const next = cur.next;
//开始交换
cur.next = prev;
prev = cur;
cur = next;
}
return prev;
};
以上算法的时间复杂度和空间复杂度分析如下:
- 时间复杂度:O(n)。
- 空间复杂度:O(1)。
既然可以使用迭代法来解决,则同样的也可以使用递归来解决,本题在递归的思路上稍微复杂一些。递归的关键点在于找到递归的条件,首先我们需要知道如果是空链表或者只有一个节点的链表是不需要进行反转的,因此递归终止的条件我们就找到了。即:
//也可以写成这样的判断head === null || head.next === null
if(!head || !head.next){
return head;
}
现在,我们用n1 ~ nk ~ nk + 1 ~ nm来代表一个链表。假定我们只反转nk 和 nk + 1,也就是说需要将nk + 1的下一个节点指向nk。那么我们应该如何做?
答案很简单,那就是将nk.next.next = nk。因此,这个表达式就是我们递归的条件,除此之外,n1的下一个节点我们应该指向为null,这样做的目的是避免产生环。根据以上分析,可以写出如下代码:
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
if(head === null || head.next === null){
return head;
}
const newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
};
以上算法的时间复杂度和空间复杂度分析如下:
- 时间复杂度:O(n)。
- 空间复杂度:O(n)。
更多思路。